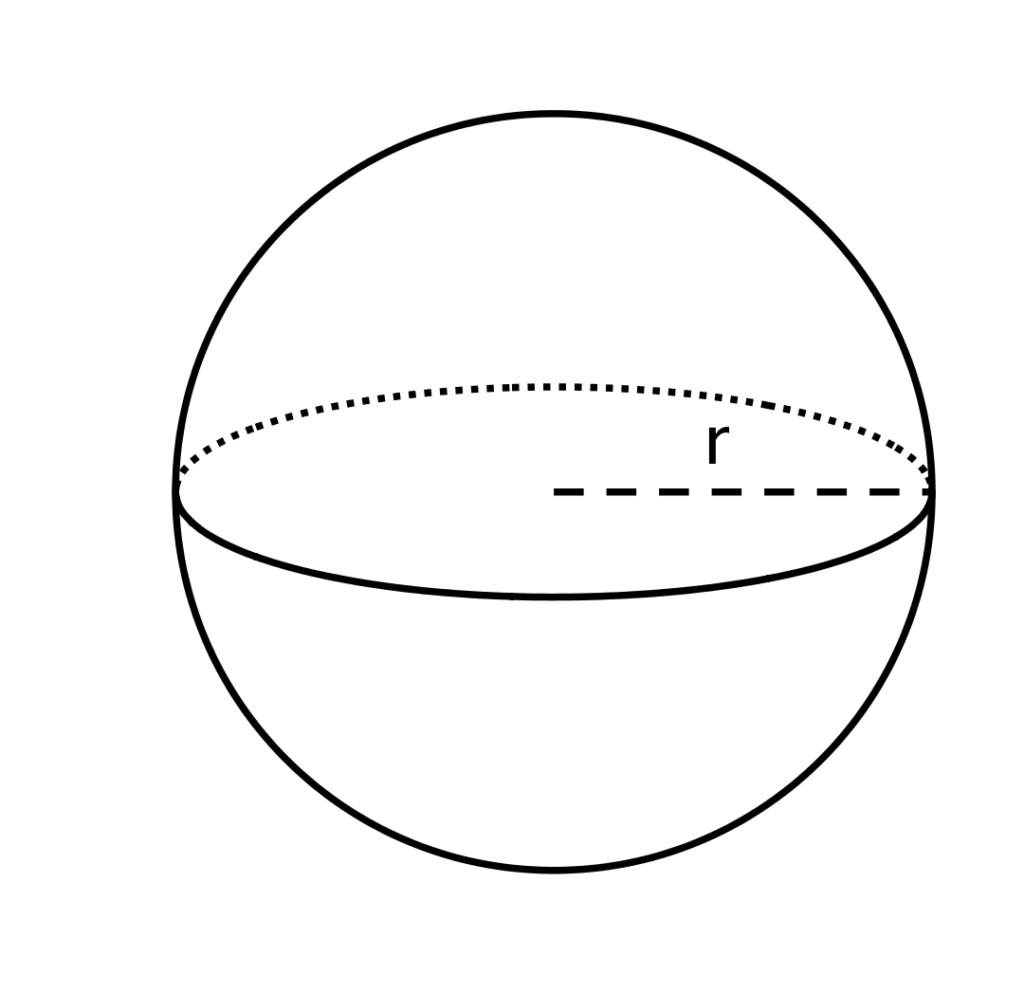
Volume Of Sphere
To calculate the volume of a sphere, you need to know its radius—the distance from its center to its surface. Then, you simply plug that number into the following formula:
Alright, since we are finding the volume of a sphere, we will be using the following volume formula: where π is a number that is approximately equals to 3.14 (or use the number given to you) and r is the radius of the sphere. The formula for the volume of a sphere is 4⁄3πr³. For a cylinder, the formula is πr²h. A cone is ⅓ the volume of a cylinder, or 1⁄3πr²h. This song’s hook makes these formulas easy to remember. The song also gives examples of objects of these shapes.
Let’s try a problem. Because a simple problem where you’re given a sphere’s radius is too easy, the following sphere problem involves a cube (just to make things interesting!): What’s the volume of a basketball in a box (technically, a cube) if the box has a surface area of 486 square inches?
A cube (or any other ordinary box shape) is a special case of a prism, but you don’t need to use the fancy-schmancy prism formula, because the surface area of a cube is simply made up of six congruent squares. Call the length of an edge of the cube s. The area of each side is therefore s2. The cube has six faces, so its surface area is 6s2. Set this equal to the given surface area of 486 square inches and solve for s:
Cossacks 3 gameplay. Thus, the edges of the cube are 9 inches, and because the basketball has the same width as the box it comes in, the diameter of the ball is also 9 inches; its radius is half of that, or 4.5 inches. Now you can finish by plugging 4.5 into the volume formula for a sphere:
(By the way, this is slightly more than half the volume of the box, which is 93, or 729 cubic inches.)